Despite developing quite independently of Babylonian mathematics, some very superior mathematical discoveries were made at a very early time in India. Mantras from the early Vedic Period (Before 1000 BCE) invoke powers of ten from a hundred all the way up to a trillion, and provide evidence of the use of Arithmetic Operations such as “Addition, Subtraction, Multiplication, Fractions, Squares, Cubes and Roots”.

During Vedic times, this decimal system, was very much in vogue in India, Yadur Veda Samhita 17th chapter, 2nd mantra describes the numerical values in a sequence like Eka, Dasa, Sata, Sahasra, Ayuta, Laksha, Niyuta, Koti, Arbud, Vrinda, Kharav, Nikharav, Shankha, Padma, Sagar, Antya, Madhya, Paradha etc. Parardha’s value is equal to 10 raised to the power 12. Indian Mathematical crown has ever-shinning gems to its credit that exists today is a gift from ancient India.

Acharya Āryabhata was born in 476 CE, He was the first of major mathematician and astronomers from the classical age of Indian mathematics and Indian astronomy. Aryabhata was born at Kusumpru (Bihar), Aryabhatt’s intellectual brilliance remapped the boundaries of mathematics and astronomy. In 499 CE, His works include the ĀRYABHAṭĪYA and the ARYA-SIDDHANTA. He wrote a text on astronomy and an unparallel treatise on mathematics called “ARYABHATIYAM.

At the age of 23” He formulated the process of calculating the motion of planets and the time of eclipses. Aryabhatt was the first to proclaim that the earth is round, it rotates on its axis, orbits the sun and is suspended in space – 1000 years before Copernicus published his heliocentric theory. He is also acknowledged for calculating π (Pi) to four decimal places: 3.1416 and the sine table in trigonometry. Centuries later, in 825 CE, the Persian mathematician, Mohammed Ibna Musa credited the value of π (Pi) to the Indians, “THIS VALUE HAS BEEN GIVEN BY THE INDIANS.” And above all, his most spectacular contribution was the concept of zero without which modern computer technology would have been non-existent. Aryabhatt was a colossus in the field of mathematics.

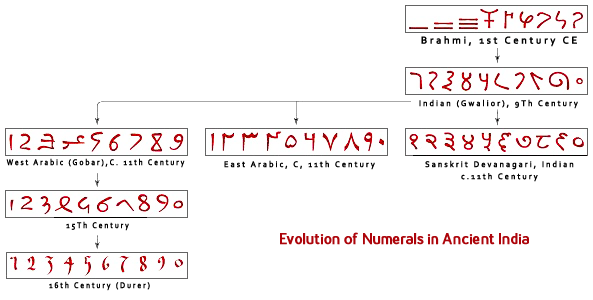
1. Decimal system: Nine numbers and a zero can be combined to form infinite mathematical expressions and measurements. This knowledge is said to be the unique contribution of ancient Indian genius to world’s progress. The place-value system, first seen in the 3rd century “BAKHSHALI” Manuscript, was clearly in place in his work. While he did not use a symbol for zero, the French mathematician Georges Ifrah explains that knowledge of zero was implicit in Aryabhata’s place-value system as a place holder for the powers of ten with null coefficients.

However, Aryabhata did not use the Brahmi numerals. Continuing the Sanskritic tradition from Vedic times, he used letters of the alphabet to denote numbers, expressing quantities, such as the table of sines in a mnemonic form. A Buddhistic text called “LALITA VISTARA” (1st century BC) describes upto 10 raised to 53 and called that numerical value as “Talakshna”. Another Jain text (anuyogadwara) describes numbers upto 10 raised to the power of 140. During the ancient periods, Greeks gave the biggest numerical value called Myriad, which is equal to 10 raised to the power of 4, i.e. 10000 only. Biggest Roman Numerical were 10 raised to 3 i.e. 1000 only. It was called as “Milli“. The numbers from zero to nine were first adopted by Arabs from India and had spread to Europe.

2. Zero Glory : Without India’s richest “zero”, the whole of mathematical knowledge becomes zero. Indians used zero not only as the mathematical expression but also as philosophical concept. Vedas, Upanishads, Puranas and many Indian classical texts had dealt with zero in various ways. Pingala (2nd century BC) in his Vedagana test “Chandas Sastra” (A guide to study Vedic prosody), while explaining Gayatri Chandas mentions zero.

3. Geometry : Geometry, an important branch of mathematics had originated in India. The word Geometry is a Sanskrit word means measuring the earth. Jya in Sanskrit means earth, miti means measurement “jyamiti” or geometry means measuring the earth. Today, what we call Pythagoras Theorem is a mere repetition of what had been said in Baudhaya “SulbaSutras”, written five to six hundred years before Pythagoras.

4. Pi π value : The value of pi had attracted the attention of every Mathematicean whether Indian or Western, ancient or modern. The pi is constant value of the ratio between the circumstance and diameter in a circle.

Aryabhata worked on the approximation for pi (π), and may have come to the conclusion that π is irrational. In the second part of the Aryabhatiyam (gaṇitapāda 10), he writes:

Caturadhikam śatamaṣṭaguṇam dvāṣaṣṭistathā sahasrāṇām

Caturadhikam śatamaṣṭaguṇam dvāṣaṣṭistathā sahasrāṇām

Ayutadvayaviṣkambhasyāsanno vṛttapariṇāhaḥ.

“Add four to 100, multiply by eight, and then add 62,000. By this rule the circumference of a circle with a diameter of 20,000 can be approached.”

This implies that the ratio of the circumference to the diameter is ((4 + 100) × 8 + 62000)/20000 = 62832/20000 = 3.1416, which is accurate to five significant figures.

It is speculated that Aryabhata used the word āsanna (approaching), to mean that not only is this an approximation but that the value is incommensurable (or irrational). If this is correct, it is quite a sophisticated insight, because the irrationality of pi was proved in Europe only in 1761 by Lambert.

5. Trignometry : Trignometry is a gift of Antient India to the mathematical world. The concepts of sign and cosign had been evolved by Indian Mathematicians. Aryabhatta had tabulated the several values of sign from 00 to 900 in his famous mathematical work Aryabhattiyam. In Ganitapada 6, Aryabhata gives the area of a triangle as

Tribhujasya Phalashariram Samadalakoti Bhujardhasamvargah

that translates to: “for a triangle, the result of a perpendicular with the half-side is the area.”

Aryabhata discussed the concept of sine in his work by the name of Ardha-Jya. Literally, it means “half-chord”. For simplicity, people started calling it jya. When Arabic writers translated his works from Sanskrit into Arabic, they referred it as jiba. However, in Arabic writings, vowels are omitted, and it was abbreviated as jb. Later writers substituted it with jaib, meaning “pocket” or “fold (in a garment)”. (In Arabic, jiba is a meaningless word.) Later in the 12th century, when Gherardo of Cremona translated these writings from Arabic into Latin, he replaced the Arabic jaib with its Latin counterpart, sinus, which means “cove” or “bay”. And after that, the sinus became sine in English.

6. Calculus : What we call today, “Calculus” was called by ancient Indians as “Kalana Ganana Sastra”. Ages before Newton had made use of it, Aryabhatta and Bhaskaracharya had dealt with his branch of Mathematics in their Astronomical calculations.

7. Algebra : This branch of Mathematics is also an Indian invention. During 9th century AD, Arabs adopted it and from them it has spread to the other parts of the world. Indian seers of yore like Apasthambha, Baudhayana and Katsyayana in his Kalpa Sutras had introduced the “unknown” value in their Mathematical expressions. Afterwards, Aryabhatta, Brahmagupta, Bhaskaracharya, Madhava and others developed various algebric formulae, equations and functions.

• In Aryabhatiya Aryabhata provided elegant results for the summation of series of squares and cubes:
• Bhaskaracharya calls Algebra as Ayaktha Ganita or Beeja Ganita. He had said that Vyaktha Ganita lead to Ayakthaganitha. In his book Leelavati he deals with vyathaganitha (arithmetic) before dealing with Ayaktha Ganitha.

Acharya Brahmaguptha was a 7th Century Indian mathematician and astronomer. He is the author of three early wrote some important works on both mathematics and astronomy. Brahmagupta was born c. 598 CE, Died c. 668 CE, He lived in the state of Rajasthan of northwest India (he is often referred to as Bhillamalacarya, the Professor from Bhillamala), and later became the Dean of the astronomical observatory at Ujjain in central India. He lived in Bhillamala (modern Bhinmal) during the reign of the Chavda dynasty ruler.

The Great Written “BRĀHMASPHUTASIDDHĀNTA” is the main work of Brahmagupta, written c. 628. Τhis text of mathematical astronomy contains significant mathematical content, including a good understanding of the role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and quadratic equations, and rules for summing series, Brahmagupta’s identity, and Brahmagupta’s theorem. Brahmagupta explained how to find the cube and cube-root of an integer and gave rules facilitating the computation of squares and square roots. He also gave rules for dealing with five types of combinations of fractions. He gave the sum of the squares of the first n natural numbers as ^{n(n + 1)(2n + 1)}⁄ 6 and the sum of the cubes of the first n natural numbers as (^{n(n + 1)}⁄₂)^².

Brāhmasphuṭasiddhānta Rules for Numbers – Treat Zero as a Number 

Brāhmasphuṭasiddhānta is one of the first books to provide concrete ideas on positive numbers, negative numbers, and zero. He wrote the following rules:

• The Sum of Two Positive Quantities is Positive
• The Sum of Two Negative Quantities is Negative
• The Sum of Zero And a Negative Number is Negative
• The Sum of Zero And a Positive Number is Positive
• The Sum of Zero And Zero is Zero
• The Sum of a Positive and a Negative is Their Difference; or, If They are Equal, Zero
• In Subtraction, The Less is To Be Taken From The Greater, Positive From Positive
• In Subtraction, The Less is To Be Taken From The Greater, Negative From Negative
• When The Greater However, is Subtracted From The Less, The Difference is Reversed
• When Positive is To Be Subtracted From Negative, And Negative From Positive, They Must Be Added Together
• The Product of a Negative Quantity and a Positive Quantity is Negative
• The Product of Two Negative Quantities is Positive
• The Product of Two Positive Quantities is Positive
• Positive Divided By Positive or Negative By Negative is Positive
• Positive Divided By Negative is Negative. Negative Divided By Positive Is Negative
• Zero Divided By A Negative Or Positive Number Is Either Zero Or Is Expressed As A Fraction With Zero As Numerator And The Finite Quantity As Denominator
• A Positive or Negative Number When Divided By Zero is A Fraction With The Zero as Denominator
• Zero Divided By Zero is Zero

The last two of these rules are notable as the earliest attempt to define division by zero, even though they are not compatible with modern number theory (division by zero is undefined for a field).

Acharya Āryabhata II (c. 920 – c. 1000) was an Indian mathematician and astronomer, and the author of the “Maha-Siddhanta” or “Āryasiddhānta”. The numeral II is given to him to distinguish him from the earlier and more influential Āryabhaṭa I.

Mahāsiddhānta or Āryasiddhānta :

The Mahāsiddhānta or Āryasiddhānta is an astronomical collection based on the traditional practice of Smṛtis (Transit from Vedic literature). The Most Eminent treatise written in Sanskrit consists of 18 Eighteen chapters and 625 Ślokas (verses). The first 12 chapters deal with chapters deals with topics related to mathematical astronomy and covers the topics that Indian mathematicians of that period had already worked on , Detailed derivations are presented on topics such as the mean and true longitudes of the planets, eclipses of the Sun and the Moon, the projections of eclipses, the lunar crescent, and the heliacal rising and settings of planets, including some calculations on conjunctions of planets as well as planets with stars.

The next six chapters of the Mahāsiddhānta form a separate section called the Golādhyāya (On the sphere) includes topics such as geometry, geography and algebra, which were applied to calculate the longitudes of the planets. In about twenty verses in the treatise, he gives elaborate rules to solve the indeterminate equation: by = ax + c. These rules have been applied to a number of different cases such as when c has a positive value, when c has a negative value, when the number of the quotients is an even number, when this number of quotients is an odd number, etc. In Chapter 17, for example, shortcuts are provided for determining the mean longitudes of the planets. In Chapter 18, under the section called Kuṭṭakādhyāya, Āryabhaṭa II discusses the topic of the solution of indeterminate equations of the first degree. He improves upon earlier methods and suggests a shorter procedure. In his work, Āryabhaṭa II also touches upon several arithmetical operations such as the four fundamental operations, operations with zero, extraction of square and cube roots, the rule of three, and fractions. To represent numbers, he adopts the famous Kaṭapayādi system of letter numerals. This practice does not conform to the method followed by some of his predecessors, who used the well‐known Bhūta Saṃkhyā system of word numerals. The text does not say anything about the year and place of Āryabhaṭa II’s birth, nor does it give any other personal information. In recent years several scholars have tried to establish an approximate period in which he lived based on the cross‐references to his work made by other contemporary and younger scholars. D. Pingee believed that Āryabhaṭa II’s treatise was written between 950 and 1100.

Acharya Bhaskara – I  was a Indian astronomer and mathematician who was the first to write numbers in the decimal system with a circle for the zero and who gave a exclusive and outstanding rational approximation of the Sine function in his commentary on Aryabhata’s work. He lived in c. 629, Possibly Valabhi, Near Modern Bhavnagar, Saurashtra, India.

Bhaskara-I’s perhaps most important mathematical role concerns the representation of numbers in a positional system. His fame rests on three treatises he composed on the works of “ARYABHATA”. Two of these treatises, known today as “MAHABHASKARIYA” (“Great Book of Bhaskara”) and “LAGHUBHASKARIYA” (“Small Book of Bhaskara”), are astronomical works in verse, while “ARYABHATIYABHASHY”A (629) is a prose commentary on the Aryabhatiya of Aryabhata.  Bhaskara particularly stressed the importance of proving mathematical rules rather than just relying on tradition or expediency. In supporting Aryabhata’s approximation to π, Bhaskara criticized the traditional use of Square root of√10 for it (common among Jain mathematicians).

Acharya Bhaskara II, also called BHĀSKARĀCĀRYA or BHASKARA was Born C.1114 in a Deshastha Rigvedi Brahmin family near Vijjadavida (believed to be Bijjaragi of Vijayapur in modern Karnataka). He lived in the Sahyadri region (Patnadevi, in Jalgaon District, Maharashtra — Died c. 1185, Probably Ujjain), the leading mathematician of the 12th century, He has been called the greatest mathematician of medieval India.

His main work “SIDDHĀNTA SHIROMANI”, (Sanskrit for “Crown of Treatises”) is divided into four parts called “LILĀVATĪ (The Beautiful)”, “BĪJAGAṇITA (Seed Counting)”, GRAHAGAṇITA ( Planet Counting) AND GOLĀDHYĀYA (SPACE STUDY), which are also sometimes considered four independent works. These four sections deal with arithmetic, algebra, mathematics of the planets, and spheres respectively. He also wrote another treatise named KARAṇAA KAUTŪHALA (“Calculation of Astronomical Wonders”).

Many of his books transliterated in several languages of the world bear testimony to its eminence. In his treatise “Siddhant Shiromani” he writes on planetary positions, eclipses, cosmography, mathematical techniques and astronomical equipment. In the “Surya Siddhant” he makes a note on the force of gravity:

“Madhye Samantandasya Bhugolo Vyomni Tisthati

Bibhranah Paramam Saktim Brahmano Dharanatmikam”

[Surya Sidhantha 12th chapter 32 sloka]

 “In the midst of universe (Brahmanda), the spherical earth stands firm in the space, because of the dharanatmika sakti, Earth is standing firm in the space without falling away.”

“Akrsta Saktisca Mahi Taya Yat Svastham Guru Svabhimukham Svasaktya

Akrsyate Tatpatativa Bhati Same Samantat Kva Patatviyam Khe”

[Sidhanta Shiromani, Bhuvanakosa, 6th sloka]

 “Objects fall on earth due to a force of attraction by the earth. Therefore, the earth, planets, constellations, moon, and sun are held in orbit due to this attraction.”

Bhaskaracharya was the first to discover gravity, 500 years before Sir Isaac Newton. He was the champion among mathematicians of ancient and medieval India. His works fired the imagination of Persian and European scholars, who through research on his works earned fame and popularity.

Indian Mathematical genius is evident from seers of Vedic times to Modern Times SRINIVASA RAMANUJAN,  P.C. MAHALANOBIS, C.R. RAO, D.R. KAPREKAR , HARISH CHANDRA  , SATYENDRA NATH BOSE , NARENDRA KARMARKAR, DR. VASHISHT NARAYAN SINGH and Many others. Today, what we call as computer language (Bakus Normal form) is a replication of “PANINI”‘s grammar rules.

Vedic Mathematics is a mathematical techniques retrieved from the Vedas